Controle Inteligente - A* Algorithm
Introdução
Este artigo expõe uma experiência realizada que consiste na implementação do algoritmo A* apresentado à disciplina de Controle Inteligente, correspondente à avaliação da a 1ª unidade do semestre 2016.1 do 9º período do curso de Engenharia de Computação e Automação da Universidade Federal do Rio Grande do Norte, UFRN, sob orientação do Prof. Fábio Meneghetti Ugulino de Araújo.
O trabalho visa além de explorar a ideia do algoritmo, realizar a apresentação do resultado de forma simples e criativa. Foi optado por implementar o software em Web, utilizando HTML5 e JavaScript, visto que existem vários plugins, templates e bibliotecas que poderiam auxiliar no desenvolvimento ágil e criativo do programa. Toda a lógica do A*, no entanto, foi desenvolvida pelo autor deste artigo.
Descrição do A* Search Algorithm
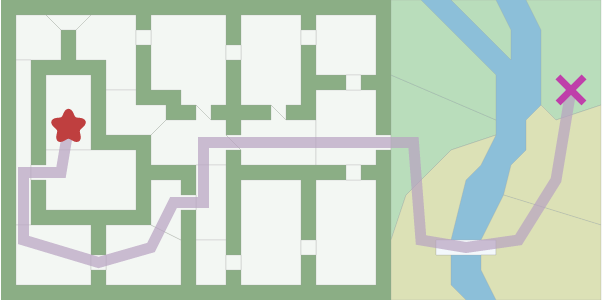
O algoritmo A* é um dos algoritmos mais simples de busca em grafo. Este utiliza a busca em largura como base do algoritmo. Ele garante encontrar um dos caminhos possíveis do ponto de partida até o ponto de chegada (caso este exista), no entanto, não garante que o caminho encontrado seja o melhor de todos.
O A* escolhe entre todos os caminhos possíveis de um determinado ponto, aquele que aparenta chegar mais rápido ao seu destino. Iniciando de um ponto de partida (Start), constrói-se uma árvore de caminhos iniciando deste nó, expande-se cada um deles a cada iteração, até que um dos caminhos expandidos seja o nó de chegada (Goal).
A cada iteração do seu loop principal, o A* determina qual dos caminhos deseja-se expandir primeiro. Para isso, ele seleciona aquele caminho que minimiza a função: $$ f'(n) = g'(n) + h'(n) $$
Onde \(g’(n)\) é a função de custo, que determina quão custoso é mover-se do ponto atual até este novo ponto de chegada. Um exemplo de custo seria o quão demorado é desloca-se de uma cidade para outra, ou então, o quão custoso é realizar uma jogada em um tabuleiro de xadrez (peças comidas x peças perdidas). Já a função \(h’(n)\) é a heurística do algoritmo, que dita o quão perto este caminho está do seu objetivo final (chegar ao ponto de destino). E por fim, a função \(f’(n)\) é a função prioridade que é a soma da função custo com a função de heurística.
Todos os caminhos que são expandidos de um determinado nó são colocados numa lista chamada de OpenQueue (fila de abertos), que armazena todos os caminhos que foram alcançados a partir dos nós visitados. Esta lista deve ser preferencialmente uma implementação de Priority Queue (fila de prioridade), pois a cada iteração do loop principal, escolhe-se o novo caminho visitado a partir dos nós que estão nesta lista e o nó escolhido é justamente aquele que possui a melhor prioridade (aquele que possui o menor valor de \(f’(n)\)).
Quando um nó é escolhido da fila de abertos, ele é retirado do conjunto de abertos (função pop()) e adicionado na fila de ClosedQueue (fila de caminhos fechados) que armazena todos os nós que foram investigados. No final da execução do algoritmo, essa fila armazenará justamente o caminho que chega até o Goal.
Esse nó que foi adicionado no conjunto de fechados, chamamos de current. No próximo passo do algoritmo, obtém-se todos os outros caminhos que são alcançáveis a partir (estes novos caminhos são chamados de vizinhos).
Para cada vizinho, é realizado os seguintes procedimentos:
- Determina-se o custo desse caminho (\(g’(n)\) do caminho atual + o custo para deslocar-se até esse caminho);
- Se esse caminho ainda não tinha sido visitado ou se ele já foi visitado, mas o novo custo
encontrado é menor do
que o último custo calculado, então faça:
2.1. Substitua o custo \(f’(n)\) antigo pelo novo custo calculado no passo 1 acima;
2.2. Determine a prioridade desse vizinho (\(g’(n)\) + \(h’(n)\));
2.3. Armazene que o nó de chegada a este nó vizinho foi a partir do current;
2.4. Adicione esse vizinho na fila de abertos, com a prioridade calculada em 2.2.
O pseudocódigo retirado do site Red Blog Games que ilustra a descrição do algoritmo é apresentado a seguir:
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost + heuristic(goal, next)
frontier.put(next, priority)
came_from[next] = current
Implementação
A implementação, como foi relatada, foi feita em Web, utilizando HTML5 e JavaScript e pode ser acessada no link dudevictor.github.io/a-star-labyrinth. Foi usada a tag canvas do HTML5 para fazer toda a exibição do resultado do algoritmo.
Uma imagem do software desenvolvido é apresentada a seguir:
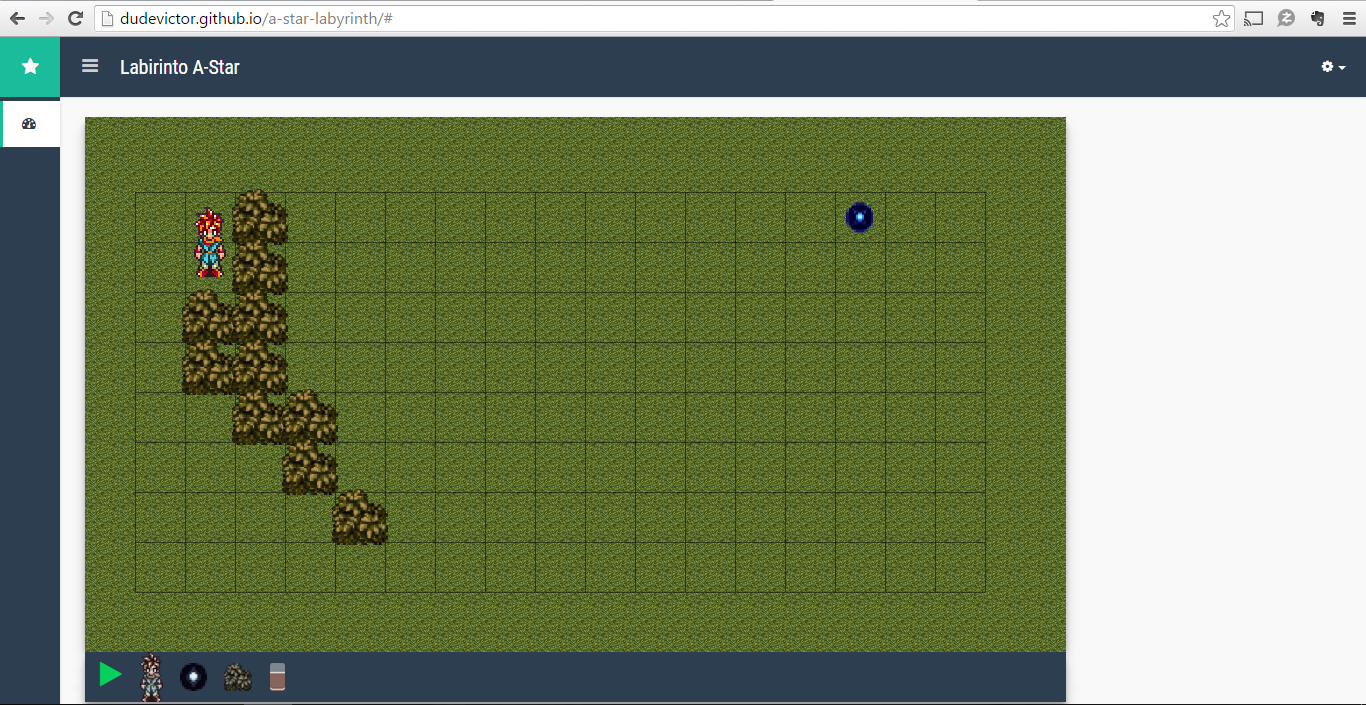
O template utilizado para compor o software foi o tui2tone e para auxiliar a exibição do resultado em formato de um jogo 2D foi utilizado a implementação canvas-game-bootstrap. Fora isso, também foram utilizados outros plugins como o jQuery, o balloon.js e sprites do jogo Chrono Trigger.
Na imagem a seguir é mostrado a execução do programa e descrito as suas funcionalidades:
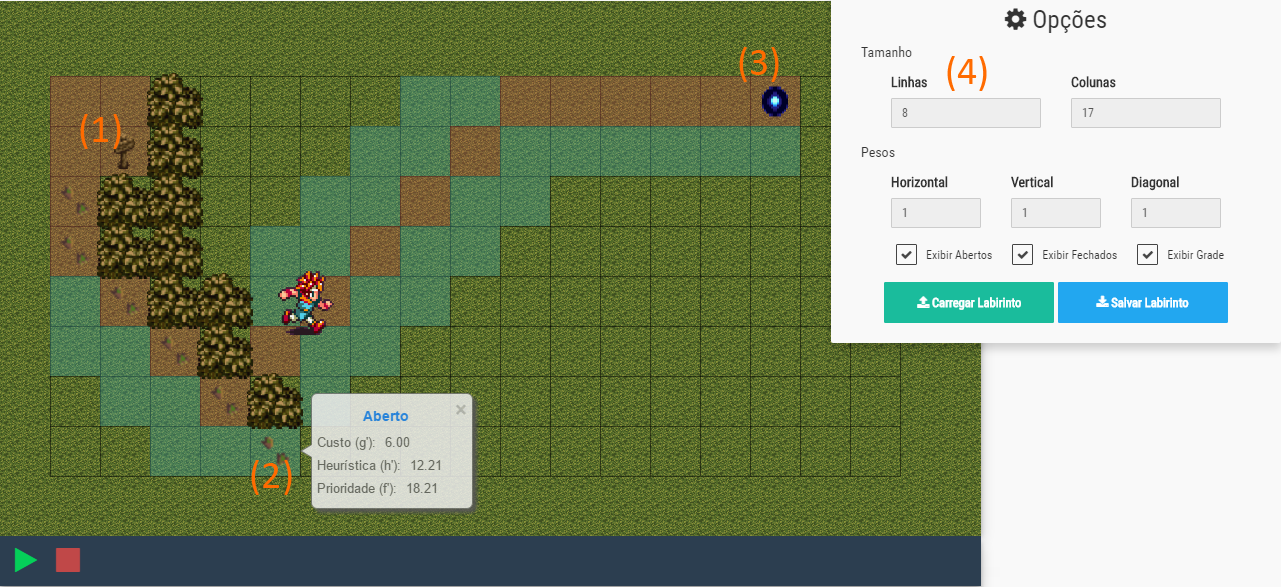
Onde:
- Ponto de Partida;
- Durante a execução do programa, é possível clicar em um dos caminhos mostrados para
exibição de alguma informações, como o caminho usado para chegar até lá e os valores das
funções \(f’(n)\), \(g’(n)\) e \(h’(n)\);
- Ponto de Chegada;
- Painel de opções para se alterar a quantidade de linhas, colunas, e os custos de deslocamento
horizontais, verticais e diagonais. Também pode-se carregar um labirinto e salvar um
labirinto em formato especificado pelo professor da disciplina;